Universal Law of Gravitation

Content:
History
It is not a secret for anyone that the law of universal gravitation was discovered by the great English scientist Isaac Newton. According to legend, he was walking in the garden. At that moment, an apple fell from the tree (in one version it fell directly on the head of a physicist, in another it simply fell). Later this apple became famous Newton’s apple. An apple that fell on Newton’s head inspired the discovery of the law of universal gravitation because the Moon in the night sky was not falling, but the apple fell. The scientist probably thought that some force acts on the Moon (causing it to rotate in orbit), and some force acts on the apple, causing it to fall to the ground.
This whole story about an apple is just a beautiful myth about how did Isaac Newton discover gravity. In fact, an apple fell or not, it is not so important. It is important that the scientist discovered and formulated the law of universal gravitation, which is now one of the cornerstones of both physics and astronomy.
Long before Newton, people observed both things falling on the ground and stars in the sky. Before him, they believed that there are two types of gravity: terrestrial (acting exclusively within the Earth, causing bodies to fall) and celestial (acting on stars and Moon). Newton was the first to unite these two types of gravity in his head, the first to understand that gravity is only one and its action can be described by a universal physical law.
Definition
What causes gravity? According to the universal law of gravitation, all material bodies attract each other, while the attractive force does not depend on the physical or chemical properties of the bodies. It depends only on the weight of the bodies and the distance between them (this is the simplest explanation). Besides this, it is necessary to take into account the fact that all bodies on Earth are affected by the force of gravity of our planet itself, which is called gravity (from Latin – gravitas).
Let us now try to formulate and write down the universal law of gravitation: the force of gravity between two objects with masses m1 and m2 and separated by distance R is directly proportional to both masses and inversely proportional to the square of the distance between them.
Equation
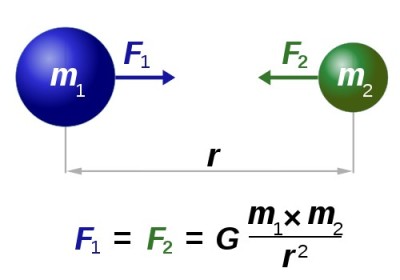
G in this formula is the gravitational constant, equal to 6,67408(31)•10−11. This is the impact on any material object of the gravitational force of our planet.
F in this formula is the force of gravity. So now you know how to find the force of gravity.
Gravitational Theory and Weightlessness in Space
The law of universal gravitation formed the basis of celestial mechanics and astronomy. Due to it, we can explain the nature of the motion of celestial bodies, as well as the phenomenon of weightlessness. Being in outer space at a considerable distance from the gravitational force of such a large body like a planet, any material object (for example, a spacecraft with astronauts on board) will be in a state of weightlessness. Since the force of gravity of the Earth (G in the gravity equation) or some other planet will no longer affect it.
References and Further Reading
- Isaac Newton: “In [experimental] philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction”: “Principia”, Book 3, General Scholium, at p.392 in Volume 2 of Andrew Motte’s English translation published 1729.
- Proposition 75, Theorem 35: p.956 – I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton’s Principia, by I.Bernard Cohen. University of California Press 1999 ISBN 0-520-08816-6 ISBN 0-520-08817-4
- The Michell-Cavendish Experiment, Laurent Hodges
- J.L. Heilbron, Electricity in the 17th and 18th Centuries: A Study of Early Modern Physics (Berkeley: University of California Press, 1979), 180.
- Discussion points can be seen for example in the following papers: N Guicciardini, “Reconsidering the Hooke-Newton debate on Gravitation: Recent Results”, in Early Science and Medicine, 10 (2005), 511-517; Ofer Gal, “The Invention of Celestial Mechanics”, in Early Science and Medicine, 10 (2005), 529-534; M Nauenberg, “Hooke’s and Newton’s Contributions to the Early Development of Orbital mechanics and Universal Gravitation”, in Early Science and Medicine, 10 (2005), 518-528.
- Bullialdus (Ismael Bouillau) (1645), “Astronomia philolaica”, Paris, 1645.
- Borelli, G. A., “Theoricae Mediceorum Planetarum ex causis physicis deductae”, Florence, 1666.
- D T Whiteside, “Before the Principia: the maturing of Newton’s thoughts on dynamical astronomy, 1664-1684”, Journal for the History of Astronomy, i (1970), pages 5-19; especially at page 13.
- H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676-1687), (Cambridge University Press, 1960), giving the Halley-Newton correspondence of May to July 1686 about Hooke’s claims at pp.431-448, see particularly page 431.
- Hooke’s 1674 statement in “An Attempt to Prove the Motion of the Earth from Observations” is available in online facsimile here.

Author: Pavlo Chaika, Editor-in-Chief of the journal Poznavayka
When writing this article, I tried to make it as interesting and useful as possible. I would be grateful for any feedback and constructive criticism in the form of comments to the article. You can also write your wish/question/suggestion to my mail pavelchaika1983@gmail.com or to Facebook.

