Moment of Inertia
The article is written by Pavlo Chaika, the chief editor of the "Piznavayka" magazine. Since its founding in 2013, Pavlo Chaika has been dedicated to popularizing science in the world. The main goal, both of the magazine and of this article, is to explain complex scientific topics in a simple and accessible language.
Content:
What is Inertia?
Inertia in physics is the ability of bodies to maintain a state of motion for a certain time in the absence of external forces. However, the concept of inertia is often used not only in physics but also in our daily lives. For instance, the inert person is the person who does not show any initiative at all. Inert persons only do what others tell them, and they do it extremely slowly, without any enthusiasm. “It moves by inertia,” we say when we want to emphasize that something is being done without any meaning, but simply because of a habit acquired over the years. Thanks to such everyday examples the concept of inertia is clear, but the term “moment of inertia” requires a more detailed explanation.
Definition
We are well aware that body mass is a measure of its inertness. For example, if in a supermarket two trolleys are pushed hard, one of which will be empty, and the second one loaded with different goods, then later it will be more difficult to stop the trolley loaded with goods due to its larger mass. In other words, the more mass the body has, the greater the effect of inertia on it, and the more forces are needed to change the movement of such a heavy body.
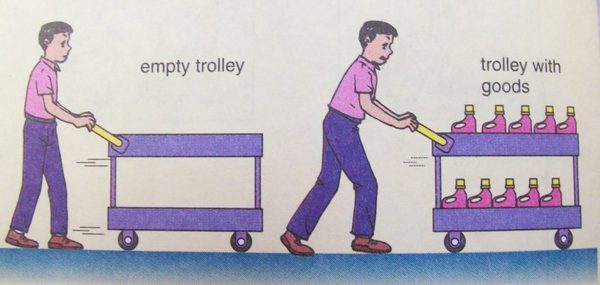
In the above example, the trolley moves in a straight line and performs a translational motion. If during the translational motion of some body its mass is a measure of its inertia, then with the rotational movement of the body around its axis, the measure of its inertia will be the quantity that is called the moment of inertia.
The moment of inertia is a scalar physical quantity, a measure of the inertia of a body when it rotates around an axis. It is usually indicated by the letter J and is measured in kilograms multiplied by a square meter.
Formula
How to calculate moment of inertia? There is a general equation that helps physicists determine the moment of inertia of any body. If the body is divided into infinitely small pieces with mass dm, then the moment of inertia will be equal to the sum of the product of these elementary masses by the square of the distance to the axis of rotation. The formula will look like this:
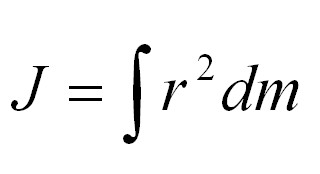
J is the moment of inertia, r is the distance to the axis of rotation.
For a material point of mass m, which rotates around an axis at a distance r, this formula will have the following form:
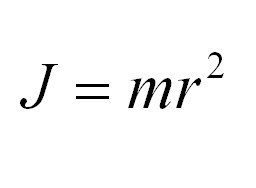
Huygens-Steiner Theorem
Speaking about the moment of inertia, it is impossible not to mention the theorem of two mathematicians Huygens and Steiner, who gave a formulation to the definition of the characteristic of parallel axes.
The Huygens-Steiner theorem states: the moment of inertia of a body about an arbitrary axis is equal to the sum of the moment of inertia of a body about an axis passing through the center of mass parallel to an arbitrary axis and the product of the mass of the body by the square of the distance between the axes.
If you write down the above mathematical formula, you get the following:
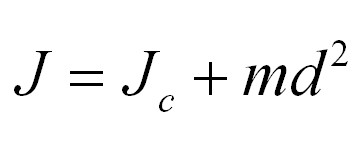
Where d is the distance between the axes
This theorem greatly facilitates the solution of many physical problems associated with inertia. For example, you have an object of arbitrary shape, the centrifugal force of which is known. Using the Steiner formula, we can calculate the moment of inertia of the body relative to any axis of a parallel line that passes through the middle of the figure.
Calculation
Despite its simplicity, the calculation of the moments of inertia for different objects requires knowledge of the integrals, these important tools of higher mathematics. To simplify the task, a table was created with inertia calculations for simple geometric shapes: circle, square, cylinder, etc.
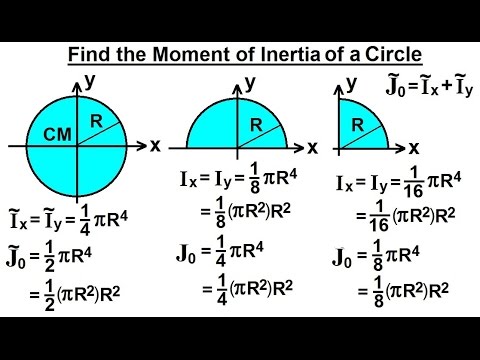
The moment of inertia for a circle is calculated this way.
The moment of inertia of a cylinder will be calculated similarly.
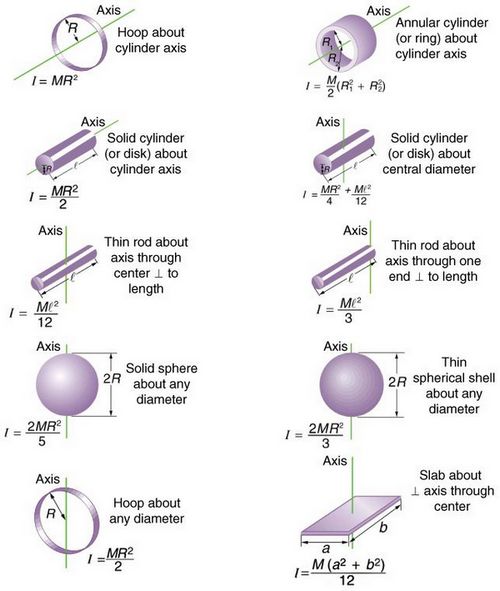
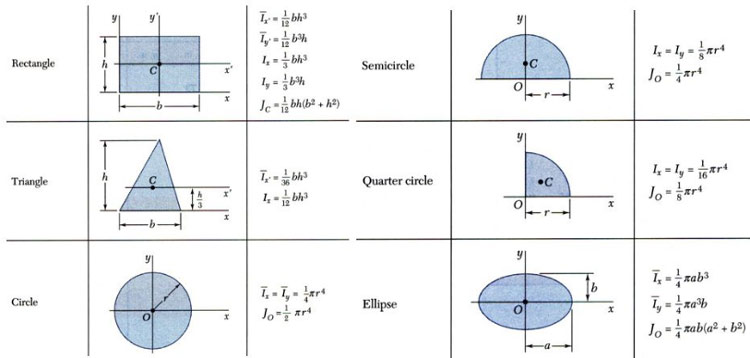
We bring to your attention more detailed tables with formulas for calculating the moment of inertia for the main geometric figures: disk, triangle, solid cylinder, etc.
References and Further Reading
- Marion, JB; Thornton, ST (1995). Classical dynamics of particles & systems (4th ed.). Thomson. ISBN 0-03-097302-3.
- Jump up to: a b Symon, KR (1971). Mechanics (3rd ed.). Addison-Wesley. ISBN 0-201-07392-7.
- Jump up to: a b Tenenbaum, RA (2004). Fundamentals of Applied Dynamics. Springer. ISBN 0-387-00887-X.
- Jump up to: a b c d e f g h Kane, T. R.; Levinson, D. A. (1985). Dynamics, Theory and Applications. New York: McGraw-Hill.
- Jump up to: a b Winn, Will (2010). Introduction to Understandable Physics: Volume I – Mechanics. AuthorHouse. p. 10.10. ISBN 1449063330.
Author: Pavlo Chaika, Editor-in-Chief of the journal Poznavayka
When writing this article, I tried to make it as interesting and useful as possible. I would be grateful for any feedback and constructive criticism in the form of comments to the article. You can also write your wish/question/suggestion to my mail pavelchaika1983@gmail.com or to Facebook.