Цікава геометрія і проблеми топології
Стаття написана Павлом Чайкою, головним редактором журналу «Пізнавайка». З 2013 року з моменту заснування журналу Павло Чайка присвятив себе популяризації науки в Україні та світі. Основна мета як журналу, так і цієї статті – пояснити складні наукові теми простою та доступною мовою.
ГНІВ БОГІВ
Знаменитий фізик Макс Борн у спогадах про свого вчителя, відомого математика Германа Міньківського наводить такий епізод: «Мінковський почав розповідь про нову математичну дисципліну з викладу так званої проблеми чотирьох кольорів. При виготовленні географічних карт з’ясувалося, що для зафарбовування будь-якої карти так, щоб дві сусідні країни були різні за кольором, необхідно і цілком достатньо мати чотири кольори.
Він додав: «На жаль, це не вдалося довести. Але цим займалися тільки математики третього рангу. Я сподіваюся цей доказ отримати», і тут він почав свої дедукції… Минуло два-три тижні, справа все ускладнювалася; і навіть через три-чотири тижні рішення не було видно. Коли ми одного ранку зібралися в аудиторії, вибухнула сильна гроза, виблискували блискавки, лив дощ. У той момент, коли Мінковський входив в аудиторію, пішов страшний удар грому. Мінковський спокійно пройшов до кафедри і сказав цілком серйозно: «Небо гнівається на мою зухвалість: мій доказ проблеми чотирьох кольорів теж невірний». Потім по його обличчю пробігла усмішка, і він знову приступив до читання лекції».
ГЕОМЕТРІЯ ГУМОВОЇ ПЛІВКИ
Завдання, яке безуспішно намагався вирішити Мінковський, здається, дуже простим. Чимало й інших настільки ж простих на вигляд завдань розглядає особлива математична дисципліна – топологія. Цікаво, що її виникнення пов’язане з рішенням «життєвого» завдання.
У Кенінсбергу було сім мостів, по яких любили прогулюватися міські жителі. Розповідають, що когось із них зацікавило питання: як вибрати шлях для прогулянки, щоб пройти по всіх семи мостах і при цьому жоден з них не перетнути двічі. Звістка про цю проблему дійшла до знаменитого математика Ейлера, який в цей час працював у Петербурзі. Ейлер вирішив її в 1735 році, довівши, що неможливо пройти по всіх семи мостах по одному разу.
Однак він зробив більше, ніж просто вирішив завдання про сім мостів. Займаючись проблемою семи мостів, Ейлер зауважив, що у геометричних фігур є властивості, які не залежать від їх розмірів і форми, а залежать тільки від загального розташування крапок і ліній. Наприклад, суть завдання про сім мостів не зміниться, якщо ми замінимо кожну частину суші точкою, а кожен міст – лінією. Тоді ми отримаємо креслення, яке ви бачите на малюнку.
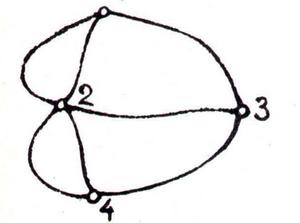
Так і вчинив Ейлер, вирішуючи завдання. Ось ці-то властивості геометричних фігур, які не змінюються при їх деформаціях, і вивчає топологія.
Твердження топології так само вірні для фігур, зроблених з гуми або намальованих на гумовій плівці, як і для жорстких фігур, з якими має справу звичайна геометрія. З цієї причини топологію можна образно назвати «геометрією гумової плівки».
Французький математик Пуанкаре сказав, що твердження топології «… залишилися б вірними, якби фігури були скопійовані невмілим креслярем, який би змінив всі пропорції і виправив всі лінії».
Завдання топологічного характеру виникали ще багато століть тому. Згідно стародавньої легенди, один халіф був так стурбований кількістю шанувальників своєї прекрасної дочки, що вирішив влаштувати для них випробування. Женихам пропонувалося завдання: з’єднати однакові цифри на фігурах, які зображені на малюнку, непересічними лініями.
Можна бути впевненим, що якби халіф не пом’якшав, його дочка ніколи не вийшла б заміж, так як це завдання не може бути вирішене. Ще в XIX столітті фізик Кірхгоф зрозумів важливість топологічних досліджень для вирішення проблем, що виникають при вивченні розгалужених електричних ланцюгів.
Цікаво, що багато важливих явищ у фізиці виявилися пов’язаними з такими ж настроями, як і ті, що фігурують в задачі халіфа. Ймовірно, самою знаменитою невирішеною проблемою після відомої теореми Ферма і, звичайно, найпростішою з вигляду є проблема чотирьох фарб, яку намагався вирішити Мінковський.
Парадоксально, що хоча проблема не була вирішена для карти, намальованої на площині або на поверхні глобуса, вона була вирішена для набагато більш складних поверхонь. Наприклад, доведено, що сім фарб необхідно і достатньо для розфарбовування будь-якої карти, намальованої на поверхні тора (фігури, що має вигляд «бублика»)
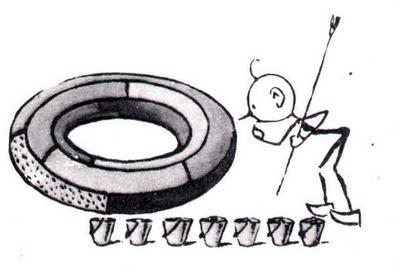
В даний час проблеми топології посилено розробляються математиками багатьох країн.
Автор: Павло Чайка, головний редактор журналу Пізнавайка
При написанні статті намагався зробити її максимально цікавою, корисною та якісною. Буду вдячний за будь-який зворотний зв'язок та конструктивну критику у вигляді коментарів до статті. Також Ваше побажання/питання/пропозицію можете написати на мою пошту pavelchaika1983@gmail.com або у Фейсбук.