Математика і краса

Прекрасний вид зоряного неба розпростертого над сонною землею. Прекрасні строгі обриси стародавнього храму, що височіє над старим містом. Прекрасні чіткі форми дорогоцінних кристалів, блискучих холодними гранями на чорному оксамиті вітрини. Прекрасні м’які лінії мармурової статуї, зробленої античним скульптором. В кожному з цих чотирьох прикладів краса заявляє про себе відразу, з першого погляду, беззастережно. Це та краса, якої не вчать на лекціях, – вона доступна “неозброєному” оку, зрозуміла непідготовленому спостерігачеві. Чи можна відкрити секрети цієї краси? З давніх-давен людина намагалася виміряти її, знайти для неї кількісні критерії.
Прекрасний вид зоряного неба…
Йоганн Кеплер, великий астроном XVI століття, який відкрив закони руху планет, вирішив піддати математичному аналізу стрункість і порядок, що панують в їхній родині. Кеплер – послідовник Коперника – твердо стояв на позиціях геліоцентризму: Сонце – центр світобудови, а навколо нього шість планет (далекі Уран, Нептун, Плутон тоді ще не були відкриті). Планети обертаються навколо Сонця майже по кругових орбітах, що лежать в одній площині. Хто визначив їм саме ці вічні шляхи навколо денного світила?

Кеплер взявся за дослідження радіусів орбіт. В результаті на світ з’явилася дивовижна конструкція зі сфер і правильних багатогранників, або, як називали їх тоді, Платонових фігур.
Найдальша з планет, відомих астрономам XVI століття,— Сатурн. Кеплер взяв сферу, радіус якої дорівнює радіусу орбіти Сатурна, і вписав в неї одну з Платонових фігур — куб, а в нього ще одну сферу, що торкається його граней. Виявилося, що радіус другої сфери дорівнює радіусу орбіти Юпітера, сусіда Сатурна. Далі кеплерові побудови йдуть так: в сферу Юпітера вписується правильний чотиригранник — тетраедр, а в нього — нова сфера, радіус якої виявляється рівним радіусу орбіти наступної планети, Марса. Проробивши цю операцію три рази і беручи з набору правильних многогранників послідовно додекаедр, ікосаедр і октаедр, можна обчислити радіуси орбіт інших членів сонячної сім’ї — Землі, Венери і Меркурія.
Звичайно, для сучасного дослідника все це не більше ніж числовий курйоз. Ніяких об’єктивних законів природи за хитромудрими побудовами Кеплера не стоїть. Та й, відверто кажучи, не такі вже вони суворі, ці побудови. Обчислені «по Кеплеру» радіуси планетних орбіт лише досить приблизно відповідають істині. А в одному місці творцеві теорії навіть довелося піти на явну підтасовку: визначаючи орбіту Меркурія, він вписав сферу в октаедр так, що вона торкнулася не граней, а ребер багатогранника. Без цієї вільності в “системі світу” не вдавалося звести кінці з кінцями.
Модель Кеплера, безумовно, заслуговує критики. Однак чудово інше; чоловік математичного складу мислення спробував висловити свої уявлення про прекрасне мовою чисел, виміряти з математичною строгістю красу, що вразила його.
Прекрасні строгі обриси стародавнього храму…
«Я не вірю,— писав Віоллє Ле Дюк, французький зодчий XIX століття, історик і теоретик архітектури,— у випадковості, особливо в області архітектури; я не вірю також і в щасливі, тобто засновані на інстинкті, поєднання. Якщо твір добрий, то це тому, що в його основі лежить хороший принцип, застосований методично».
Іншими словами, щоб створювати прекрасне, зодчий повинен знати формули краси і володіти ними. Як кажуть математики, вірно і зворотне: «Зізнайтесь, що було б дивно, якби архітектура, дочка геометрії, не могла довести геометрично, чому око мучить недолік в пропорціях будь-якої будівлі…» – читаємо у того ж Ле Дюка.
Сказане легко проілюструвати прикладами. Так і тягне почати з єгипетських пірамід. Але, власне кажучи, тут і поширюватися не про що: тут геометрія, одна геометрія, ні чого, крім геометрії в камені.

Стародавня Греція, Парфенон, інший визнаний зразок прекрасного в архітектурі, набагато більш складна споруда, але за всім різноманіттям його форм — прості, прозорі геометричні співвідношення. Щоб виявити їх, нам доведеться кілька рядків присвятити просторовим побудовам.

Візьмемо правильну чотиригранну піраміду, у якій найменший за площею перетин, що проходить через вершину, являє собою рівносторонній трикутник. Витягнемо з неї найбільший перетин, що проходить через вершину, — трикутник, підставою якого служить діагональ квадратного “днища” піраміди. Основу цього трикутника розіб’ємо на частини вісьмома зарубками — за кількістю колон на фасаді Парфенону. Там, де вертикальна вісь третьої колони (А) перетне бічну сторону трикутника, проведемо лінію паралельну основі (В). Це і буде нижній край портика. Ще кілька лінії, і перед нами схематичним малюнок фасаду знаменитого храму.
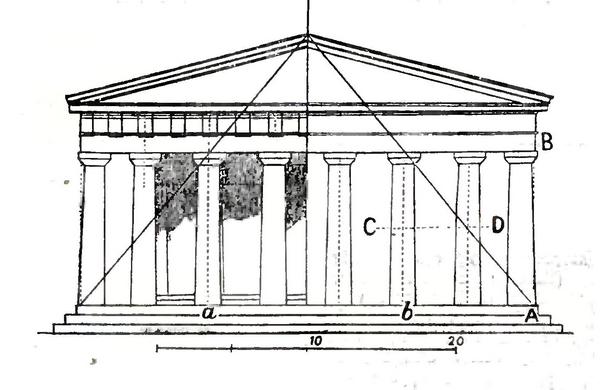
Подібні розкладання на елементарні геометричні форми здійсненні для багатьох прославлених своєю красою споруд — і старовини і ближчих часів. Прикладів тому безліч, тих, що цікавляться можна відіслати до підручників і посібників з архітектури, монографій з теорії та історії зодчества.
Прекрасні м’які лінії мармурової статуї…

Перед нами робота класика грецької скульптури Поліклета «Діадумен» («Той, що одягає пов’язку»). У ній Поліклет втілив у бронзі свої естетичні концепції, детально викладені в його праці “Канон”. На жаль, книга загубилася в століттях. І ось Леон-Баттіста Альберті, італійський художник та архітектор XV століття, задумав розгадати секрети античних майстрів. Стародавній митець, вважав Альберті, «створюючи зображення богині, запозичив у найвидатніших по красі дівчат все, що в кожній з них було найбільш витонченого і вишуканого в сенсі краси форм, і переносячи це у свій твір. Так під різцем скульптора виникав образ вищої, рафінованої краси, якою природа обдарувала багато тіл, як би розподіливши її між ними».

Усвідомивши це, Альберті провів систематичне дослідження параметрів «ідеальної фігури»: «..Ми обрали ряд тіл, найбільш красивих по судженню знавців, і від цих тіл запозичили наші виміри, а потім, порівнявши їх один з одним і відкинувши відхилення в ту або іншу сторону, ми обрали ті середні величини, які підтвердилися збігом цілого ряду вимірювань». (Що ж, цілком строгий і переконливий метод з точки зору сучасної математичної статистики!).
Ось деякі результати: якщо зріст ідеально складеної людини розділити на 60 умовних частин — дюймів, то відстань від сліду ступні до пупа складе 36 дюймів, до найдовшого пальця при опущеній руці — 23 «дюйма», ширина між кутами плечей — 15 дюймів і т. д.
У 1528 році з’явилася книга великого німецького живописця Альбрехта Дюрера «Про людську пропорцію». Дюрер відомий нам не тільки як художник, але і як людина, не чужа математиці (йому, наприклад, належить витончений, хоча, зрозуміло, наближений спосіб трисекції кута). У своєму трактаті Дюрер, систематизуючи накопичені на той час знання, спробував звести красу людського тіла до суворих пропорцій. Канони, за якими воно складено, на думку живописця-математика, такі: висота обличчя становить 1/10 від росту, висота голови — 1/8, ширина плечей — 1/4, ширина грудей — 1/6 і т. д. Важливе місце в своїй системі співвідношень Дюрер відводив так званому «золотому перетину».

Альбрехт Дюрер, автопортрет.
Саме в цій знаменитій пропорції ріст людини ділиться лінією пояса, а також лінією, проведеною через кінчики середніх пальців опущених рук, нижня частина обличчя — ротом і т. д.
«Золотий перетин» (тобто поділ відрізка на такі частини, які відносяться один до одного так само, як найбільший до цілого) веде свою історію від піфагорійців, що обожнювали число і бачили в ньому основу світобудови. Чудове співвідношення, недарма прозване золотим, захоплювало і саме по собі, своєю математичною витонченістю.
Так зійшлися досконалість людського тіла і краса математичного співвідношення. Зійшлися і доповнили один одного: формула знайшла чарівний образ, тілесна краса підтвердилася абстрактною формулою. Цікавий і знаменний факт!
Прекрасні чіткі форми дорогоцінних кристалів…

На фотографії — кристали алмазу. У кожного — вид правильного восьмигранника — октаедра. Навіть випускнику середньої школи під силу написати рівняння його поверхні:
|Х|+|У|+|Z|=1
Математична простота цього виразу не випадкова. За нею чітко проглядаються фізико-хімічні закономірності, керуючі зростанням кристалів. У процесі вільного повільного зростання кристал завжди приймає сувору форму багатогранника.
Власне кажучи, математика і зорова, наочна краса дружать давно. У XVII столітті Рене Декарт запропонував зображати математичні рівняння у вигляді графіків. Виявилося, що прості канонічні співвідношення, втілені в графічну форму, ставали витонченими фігурами. Просто язик не повертався іменувати їх сухими термінами. Тоді-то і з’явилися романтичні назви «кардіоїда» (подібна серцю), «астроїда» (зіркоподібна), «лемні ската» (прикрашена стрічками), «локон Марії Аньєзі», «декартів лист»…
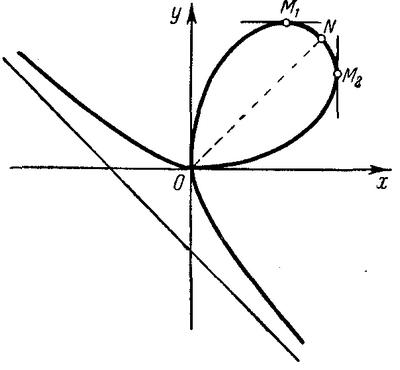
Декартів лист.
До слова, про останній термін “декартів лист” належить послідовникам великого математика. Сам Декарт називав цю химерну лінію більш поетично: “пелюстка жасмину”.
В даному випадку, як кажуть математики, вірно і зворотне. Красиві, правильні обриси листя, якими природа наділила рослини, як правило, описуються простими і витонченими математичними формулами. Ця дивовижна обставина склала тему солідного трактату «аналітичні форми листя» (Л. Хабеніхт, 1896 рік).
«Прекрасно те, що подобається без інтересу», говорив мудрий Кант. Можна сперечатися про естетичну цінність всіх цих зразків «математичної творчості», але люди мистецтва – художники, оформлювачі, ілюстратори – давно вже звертаються до цього джерела своєрідної суворої краси.
Автори: Ю. Попов, Ю. Пухначев.

