Математична мозаїка
Стаття написана Павлом Чайкою, головним редактором журналу «Пізнавайка». З 2013 року з моменту заснування журналу Павло Чайка присвятив себе популяризації науки в Україні та світі. Основна мета як журналу, так і цієї статті – пояснити складні наукові теми простою та доступною мовою.
До сих пір нас захоплює прикладне мистецтво древніх: стіни храмів, прикрашені вигадливою мозаїкою, химерні орнаменти східних килимів. Народним умільцям не були відомі закони геометрії. Скільки часу потрібно було їм, щоб домогтися чітких і правильних форм! Свої методи вони тримали в секреті, передавали з покоління в покоління. Тим часом ці малюнки можуть складатися з різних сполучень простих геометричних фігур – трикутників, багатокутників, квадратів.
Математична мозаїка може бути «правильною» та «напівправильною». «Правильна» мозаїка складається з однакових і абсолютно рівних фігур. Причому існує тільки три види такої мозаїки: системи рівнобедрених трикутників, квадратів і правильних шестикутників. Поєднання шестикутників будуються за принципом бджолиних сот.
«Напівправильні» мозаїки утворені різними поєднаннями з трикутників, квадратів, восьмикутників і дванадцятикутників. Тут вже більша різноманітність. Але і в «напівправильній» мозаїці кількість візерунків зовсім визначена – 8. З них мозаїка А має дві форми – пряму і зворотну, її дзеркальне відображення. Сім інших при відображенні в дзеркалі не міняються.
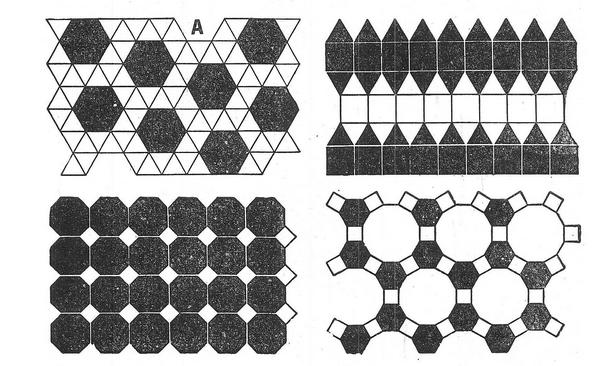
Всі мозаїки, що покривають поверхню повторюваним візерунком, належать до системи з 17 різних симетричних груп. Ця система і вичерпує всі можливості нескінченного повторення візерунка у двох вимірах. Вперше її розробив і науково обґрунтував в 1891 році російський кристалограф Є. С. Федоров.
Крім мозаїк, візерунок яких складається з геометричних фігур, існує ще один цікавий вид мозаїки, де неправильні, але абсолютно однакові предмети – люди, тварини, квіти і т. д. – розташовані таким чином, що проміжки між ними утворюють такі ж точно предмети.
Автор: Павло Чайка, головний редактор журналу Пізнавайка
При написанні статті намагався зробити її максимально цікавою, корисною та якісною. Буду вдячний за будь-який зворотний зв'язок та конструктивну критику у вигляді коментарів до статті. Також Ваше побажання/питання/пропозицію можете написати на мою пошту pavelchaika1983@gmail.com або у Фейсбук.