Геометрія Всесвіту

Перш ніж розповідати про щось з області сучасної науки, треба домовитися уважно обмірковувати всі аргументи і по можливості не вдаватися до слова «очевидно». Це – дуже небезпечне слово. В давнину здавалося, очевидно, що Земля не може бути кулею. «Інакше, – говорили вчені – скептики, – люди з іншого боку мали б ходити вниз головою, і вони б впали – це ж очевидно!» У наш час у школі без особливої праці пояснюють навіть маленьким учням і ученицям, що Земля куляста, і не падають люди з неї тому, що поняття «верх» і «низ» на Землі не мають абсолютного сенсу і є не цілком точним вираженням напрямків до центру планети і від нього. І нам тепер очевидно, що Сонце не може щовечора занурюватися у світовий океан, який нібито оточує Землю-млинець, що Земля не може стояти на трьох китах і т. д.

Не тільки фізика з’ясовувала, що природа влаштована зовсім не так, як «бачать очі». До цього висновку приводить нас вся діяльність людини. Щоб пізнати властивості оточуючого нас світу, треба ретельно переробити інформацію, яку отримують органи чуття. І найголовніший урок, який дала нам природа, полягає в тому, що тільки правильно поставлений дослід може з’ясувати фізичну сутність явищ і що ніякі теоретичні побудови, якими б вони не здавалися очевидними, але можуть без досліду відповісти на питання, що стосуються устрою фізичного світу.

Якщо все, що тут сказано, не викликає заперечень, ми можемо перейти до нашої основної теми.

У школі вчать геометрію Евкліда. Визначають точку, пряму, площину аксіомами і не помічають, що правильність опису цими аксіомами результатів вимірювань у реальному світі нізвідки не слідує. Пізніше ці аксіоми переносяться в механіку, і знову питання про перевірку їх на досліді не з’ясовується. Але будь-яка теорія повинна бути перевірена на досліді, і особливо – висновки геометрії Евкліда. Дійсно, звідки ми знаємо, що сума кутів трикутника дорівнює 180? Якщо виміряти з великою точністю кути трикутника, побудованого на футбольному полі, то це виявиться так. Але якби ми побудували трикутник, помістивши одну вершину на Північному полюсі, а дві інших – на екваторі (на довготі Грінвіча і на 90 східної довготи), то в такому трикутнику кожен кут дорівнюватиме 90 ° і, отже, їх сумі – 270 °.

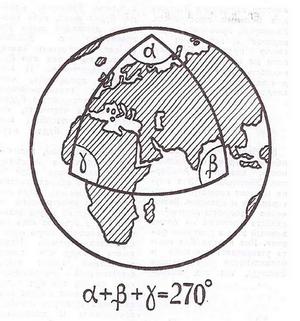
Можуть заперечити; в шкільній теоремі говориться про плоский трикутник, а не про трикутник, намальований на поверхні кулі. Але, будуючи трикутник на поверхні Землі (для наочності глобуса), ми теж проводимо «прямі лінії» – найкоротші між двома точками лінії на сферичній поверхні. Це дуги великого кола.

Властивості поверхні кулі, одну з яких ми зараз розглянули, і утворюють геометрію сфери. Ми бачимо, що геометрія сфери відрізняється від геометрії площини, і неважко зрозуміти, що кожна поверхня має свою геометрію. На прикладі суми кутів трикутника ми бачимо, крім того, що можна вивчати геометрію поверхні, не йдучи з неї самої, а лише вимірюючи характеристики фігур, намальованих на ній. Принаймні, в принципі можна отримати всі відомості про поверхню земної кулі, роблячи на ній геодезичну зйомку.

У СВІТІ ТРЬОХ ВИМІРЮВАНЬ

Ми порівняно легко можемо переконатися в різних властивостях сфери і площини. У тривимірному світі картина значно складніше. Задамося знову питанням: чому дорівнює сума кутів трикутника, вершини якого лежать, наприклад, на Сонці, Сіріусі і на найближчій до нас зірці – Альфа Центаврі. За геометрії Евкліда сума кутів трикутника дорівнює 180. Але як перевірити таке твердження? Посилання на те, що досліди на Землі підтверджують теорему, нічого не доводить. Справедливе на малих відстанях може виявитися невірним для великих.

На прикладі сферичного трикутника ми бачили, що відхилення від властивостей плоских трикутників тим більше, чим більше трикутник. З іншого боку, у нас немає ніяких способів виміряти суму кутів такого великого трикутника. Більше того, навіть ці відстані можуть виявитися недостатніми, щоб виявити відхилення від законів геометрії Евкліда. Звідси випливають два висновки. По-перше, у нас немає доказів справедливості геометрії Евкліда для великих просторів. По-друге, перевірити справедливість геометрії не так-то просто. Тому, якщо не посилатися на очевидність, треба шукати шляхи для експериментального дослідження питання.

ПРОСТІР І ЧАС

Проблема була вирішена загальною теорією відносності, створеної Альбертом Ейнштейном. Ця наука вивчає геометрію простору і часу. Включення до питання геометрії властивостей часу – дуже важливий етап у розвитку науки. Як не можна без досліду стверджувати що-небудь про правильність геометрії Евкліда, так само, виявляється, у нас немає ніяких підстав вважати, що геометричні властивості нашого світу представляються однаковими рухомому спостерігачеві і спостерігачеві, що знаходиться в спокої.

Спеціальна теорія відносності встановила, що рухомі тіла скорочуються в напрямку руху. Тому вимірювання відстані між двома точками в просторі за допомогою натягнутої мотузки або ж по часу, який треба затратити для переїзду з однієї точки в іншу з відомою швидкістю, дає різні результати. Різниця, правда, буде малою, якщо швидкість руху мала в порівнянні з 300 000 км/сек. – швидкістю світла, але, тим не менше, вона буде існувати. І ми повинні передбачати, що перевірка геометричних властивостей простору буде залежати, зокрема, від того, яким способом ми ці властивості будемо вивчати.

Таким чином, геометрія і рух виявляються зв’язаними один з одним. Цю обставину і мають на увазі, коли говорять, що простір і час один від одного залежать. Часто говорять ще про чотиривимірний світ «простір – час». Треба мати на увазі, що такий вираз має лише формальний математичний сенс, оскільки зрозуміло, що ні в яких дослідах чи явищах просторові координати і показання годин не можуть бути переплутані.

ПРЯМА ЛІНІЯ

Щоб вивчати геометрію світу, треба, насамперед, вміти провести пряму лінію. Це можна зробити різними способами. Можна просто натягнути нитку між двома точками. Можна прокреслити пряму лінію як траєкторію тіла, що рухається за інерцією. Можна, нарешті, прямою лінією назвати шлях променя світла. У звичайних, земних умовах ми повинні стежити, щоб вона не провисала, щоб вага її була малою і земне тяжіння практично не змінювало її форму. Спостерігаючи за рухом тіла, ми повинні бути впевнені, що на нього не діють ніякі сили і воно дійсно рухається за інерцією. Нарешті, коли ми будемо виробляти побудову за допомогою променя світла, необхідно перевірити оптичну однорідність середовища, щоб бути впевненим, що світло не заломлюється. Як би ми не починали побудову, ми відразу ж йдемо від чистої геометрії і повинні виробляти справжній фізичний дослід.

У такому досліді насамперед виявиться, що його результати не абсолютно точні, а його супроводжує якась, нехай навіть і дуже невелика, помилка. На відміну від геометричних аксіом, які точні за визначенням, геометрію реального світу ми визначимо лише приблизно. Ясно, що, проводячи дослід не в земних, а в космічних умовах, важко дотримуватися всіх перерахованих правил. Тому досліди мають бути поставлені так, щоб вони навіть при невеликій точності дозволили якісно вивчити геометрію.

Основним висновком загальної теорії відносності було твердження, що геометрія нашого світу не евклідова. Відхилення від законів геометрії Евкліда позначається насамперед у тому, що тіло при відсутності зовнішніх сил рухається не по прямій. Таке відхилення траєкторії від прямої сприймається спостерігачем як рух тіла під дією якоїсь зовнішньої сили, яку звикли називати силою тяжіння. Це означає, що тяжіння різко відрізняється від інших сил, які діють в природі, електромагнітних та ядерних. Спостерігач описує рух тіл поняттями геометрії Евкліда і механіки Ньютона і будь-які відхилення від теорем цих наук пояснює наявністю нових сил. Зведення сил тяжіння до геометричних властивостей Всесвіту дозволило вирішити одну з найскладніших проблем природознавства. У зв’язку з цим загальну теорію відносності часто називають теорією тяжіння.

Далі буде.

Автор: А. Я. Смродінський.