Математическая мозаика
Статья написана Павлом Чайкой, главным редактором журнала «Познавайка». С 2013 года, с момента основания журнала Павел Чайка посвятил себя популяризации науки в Украине и мире. Основная цель, как журнала, так и этой статьи – объяснить сложные научные темы простым и доступным языком
До сих пор нас восхищает прикладное искусство древних: стены храмов, украшенные затейливой мозаикой, причудливые орнаменты восточных ковров. Народным умельцам не были известны законы геометрии. Сколько времени нужно было им, чтобы добиться четких и правильных форм! Свои методы они держали в секрете, передавали из поколения в поколение. Между тем эти рисунки могут составляться из различных сочетаний простых геометрических фигур — треугольников, многоугольников, квадратов.
Математическая мозаика может быть «правильной» и «полуправильной». «Правильная» мозаика состоит из одинаковых и абсолютно равных фигур. Причем существует только три вида такой мозаики: системы равнобедренных треугольников, квадратов и правильных шестиугольников. Сочетания шестиугольников строятся по принципу пчелиных сот.
«Полуправильные» мозаики образованы различными сочетаниями из треугольников, квадратов, восьмиугольников и двенадцатиугольников. Здесь уже большее разнообразие. Но и в «полуправильной» мозаике количество узоров совершенно определенное — 8. Из них мозаика А имеет две формы — прямую и обратную, ее зеркальное отражение. Семь других при отражении в зеркале не меняются.
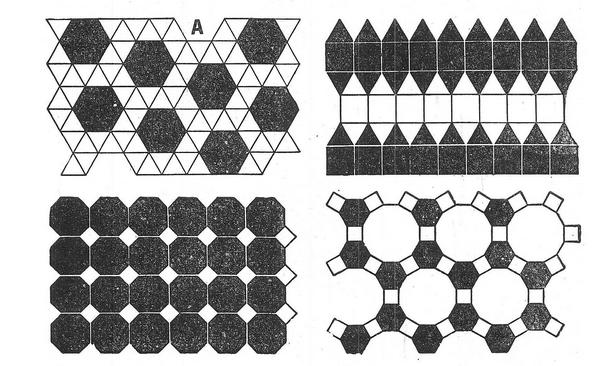
Все мозаики, покрывающие поверхность повторяющимся узором, принадлежат к системе из 17 различных симметрических групп. Эта система и исчерпывает все возможности бесконечного повторения узора в двух измерениях. Впервые ее разработал и научно обосновал в 1891 году русский кристаллограф Е. С. Федоров.
Кроме мозаик, узор которых состоит из геометрических фигур, существует еще один интересный вид мозаики, где неправильные, но совершенно одинаковые предметы — люди, животные, цветы и т. д. — расположены таким образом, что промежутки между ними образуют такие же точно предметы.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.